1.3.3 一般的方法としての手続き

文責:@naoiwata

本節の目的

下記の 2 つの例を用いながら更に強力な抽象化の手法を学ぶ.

• 区間二分法による方程式の零点の探索
• 関数の不動点の探索

区間二分法による方程式の零点の探索

区間二分法(Half-Interval Method) とは連続関数 f に対して \(f(x) = 0\) の根を探す場合に有用な手法のひとつである.

2 点 a, b が \(f(a) < 0 < f(b)\) を満たす時, f は a と b との間に少なくとも 1 つの零点を持つ.

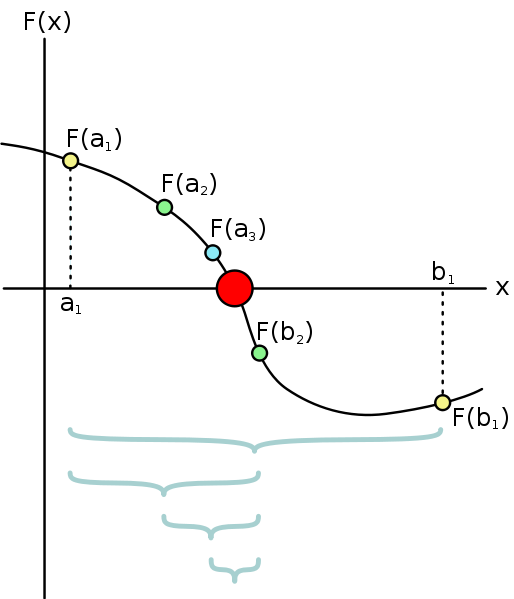
まず \(f(a) < 0\), \(0 < f(b)\) を満たす a, b を用意する. 二分法を繰り返し, ある許容誤差(T) より小さい時解とする.

図で示すように, このアルゴリズムのステップ数は,

解となる n 回目において, \(\frac{L}{2^n} = T\) が成り立つとすると, \(n = log \frac{L}{T}\) となり, ステップ数は a と b の差である L と許容誤差 T に依存することが分かる.

(define (search f neg-point pos-point)
  (let ((midpoint (average neg-point pos-point)))
    (if (close-enough? neg-point pos-point)
        midpoint
        (let ((test-value (f midpoint)))
          (cond ((positive? test-value)
                 (search f neg-point midpoint))
                ((negative? test-value)
                 (search f midpoint pos-point))
                (else midpoint))))))

search 手続きは, 引数に探索対象の関数 f と, a, b に相当する neg-point, pos-point を引数に受け取り, 解を返す.

関数の不動点の探索

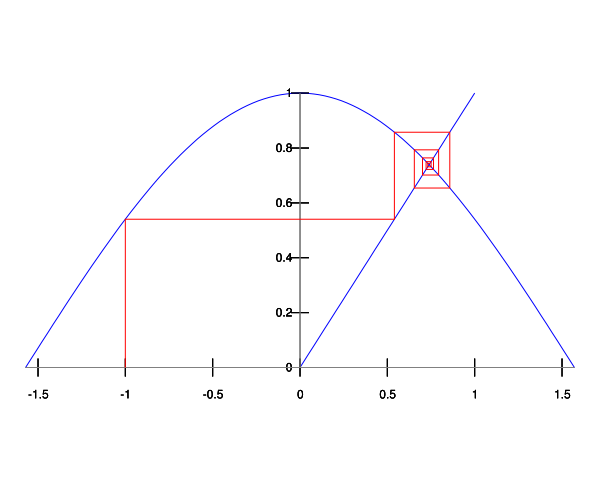
ある x において \(f(x) = x\) を満たす時, x は f の不動点(Fixed-Point)と呼ぶ. 不動点の探索は, ある予測値をまず設定し, f を繰り返し作用させ値がある許容誤差以内になった値を解とする.

(define (fixed-point f first-guess)
  (define (close-enough? v1 v2)
    (< (abs (- v1 v2)) tolerance))
  (define (try guess)
    (let ((next (f guess)))
      (if (close-enough? guess next)
          next
          (try next))))
  (try first-guess))

fixed-point 手続きは, 引数に探索対象の関数 f と初期の予測値を引数に受け取り解を返す.

これを用いて, 例えば \(cos(x) = x\) となる x の値を (fixed-point cos 1.0) を計算することで求められる.

不動点探索には平均緩和法が有用である

ここで, ある実数 a における平方根 \(\sqrt{a}\) を考えよう. \(\sqrt{a}\) とは, \(y^2 = a\) を満たす y の値を探すことと同意である.

即ち,

\(y^2 = a\)

\(y = \frac{a}{y}\)

このとき

y は \(y \mapsto \frac{a}{y}\) の不動点を探索する, と言う.

sqrt は以下のように定義でき, 手続きを追ってみる.

(define (sqrt x)
  (fixed-point (lambda (y) (/ x y))
               1.0))

• (fixed-point (lambda (y) (/ x y)) 1.0))
• (try 1.0)
• (f 1.0) ;; => (lambda (y) (/ x y))
• (try 1.0)
• (f 1.0) ;; => (lambda (y) (/ x y))

無限ループになり解を導出できない.

この解決策として 平均緩和法(Average Damping) がある. 平均緩和法は予測値の大きな変化を防ぐことで, 解への逐次近似値を平均化する方法で, 不動点探索で収束を助ける有用な方法のひとつである.

\(y^2 = a\)

\(y = \frac{a}{y}\)

\(y + y = \frac{a}{y} + y\)

\(2y = \frac{a}{y} + y\)

\(y = \frac{1}{2}(\frac{a}{y} + y)\)

即ち

\(y \mapsto \frac{1}{2}(\frac{a}{y} + y)\)

(define (sqrt x)
  (fixed-point (lambda (y) (average y (/ x y)))
               1.0))

この手続きを追って見る.

• (fixed-point (lambda (y) (average y (/ x y))) 1.0)
• (try 1.0)
• (avarage 1 (/ x 1))
• (try (avarage 1 (/ x 1)))
• (average (avarage 1 (/ x 1)) (/ x (avarage 1 (/ x 1))))

次の予測値を \(f(x) = x\) を満たす x でなく, 予測値と \(f(x) = x\) の平均値にすることで無限ループを防いだ.

まとめ

上の 2 つの例を用いながら, ある関数に対して目的の解を計算する為に, 引数として手続きが渡せる高階手続きを用いることで, 更に抽象度を上げプログラムの表現力を広げられることを示した.